An In-depth Look at the Four Key Aspects of Variography

A comprehensive guide to variography featuring tips on preparing, calculating, modelling, and interpreting. Get actionable insights on mastering this important technique with Supervisor!

Variography merges the science of data comparison, the intuition of geology and the art of modelling to communicate a geologist’s understanding of grade continuity. Understanding how sample grade values relate to each other in space can help to infer possible similarities between known samples and points that have not been sampled. This information can then be used to generate an estimate (for example, using ordinary kriging) of the grade at unsampled locations. Variography is a powerful tool that allows geologists to communicate their understanding of the grade continuity.

Variography encompasses four main aspects:

• Preparing
• Calculating
• Modelling
• Interpreting

Each step is crucial in ensuring accurate and meaningful results.

Preparing: The Foundation for Accuracy

The accuracy of continuity directions and variogram modelling parameters relies on a solid understanding of the controls on mineralization. A resource analyst must grasp the structural, weathering, and lithological factors that influence mineralisation.

Clear domaining leads to clear variography. Establishing clear domains is essential for simplified and effective variography. Poor domaining results in confusing variograms and incompatible variogram models for estimation.

Calculating

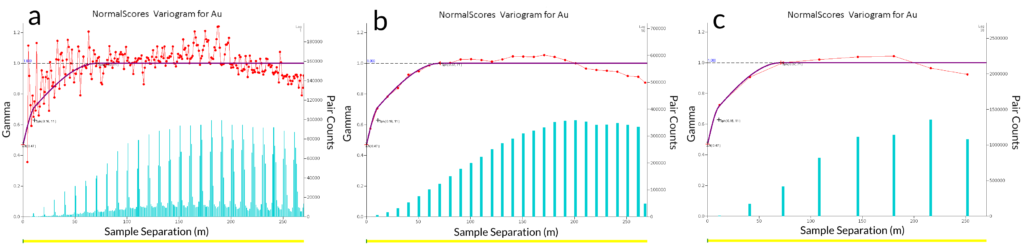
Plotting differences between sample values against separation distance provides crucial insights. Samples further apart are expected to be more different from each other than those in close proximity. An experimental variogram is created by plotting the average variability for all sample pairs at a certain distance apart against that separation distance, termed the lag or “h” (e.g. 10 m). When calculating a directional variogram, “h” refers to the distance and direction vector (e.g. 10 m north-south).

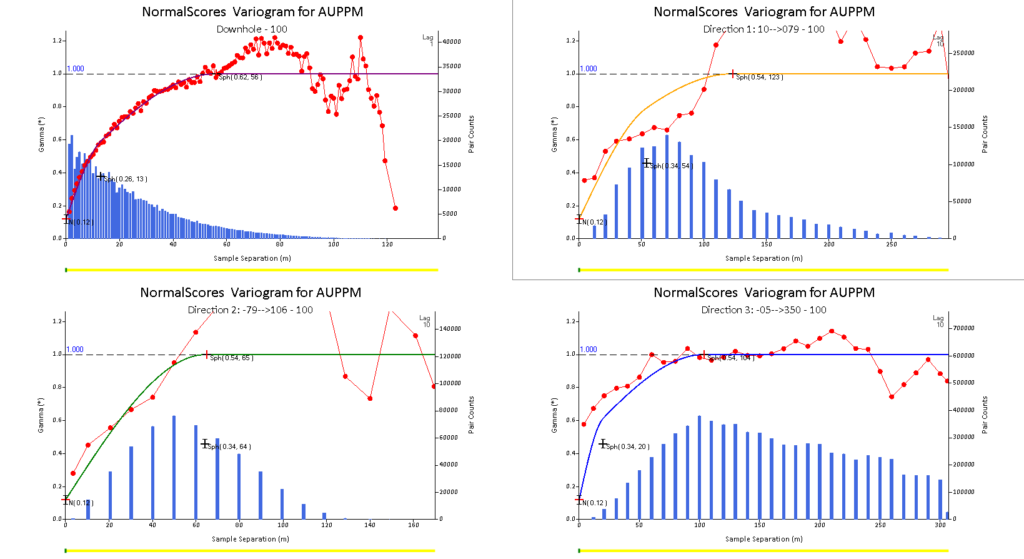
The gamma symbol (Ɣ) is the standard symbol for the variogram values. On the variogram we plot Ɣ (h), which is the average variability (or variogram value) of all sample pairs separated by vector “h”. The average variability is calculated for a series of lags and plotted against the lag distance to create a variogram plot. Using the nominal drill spacing is a good starting point to select the lag value. Superimposing the pair count on the variogram can also be used as a guide for assessing the lag value (Figure 1).

Modelling

In order to use a variogram for estimation, the experimental variograms need to be modelled in three orthogonal directions that define a three-dimensional ellipsoid. The three directions are called the major (direction 1), semi-major (direction 2) and minor (direction 3) axes.

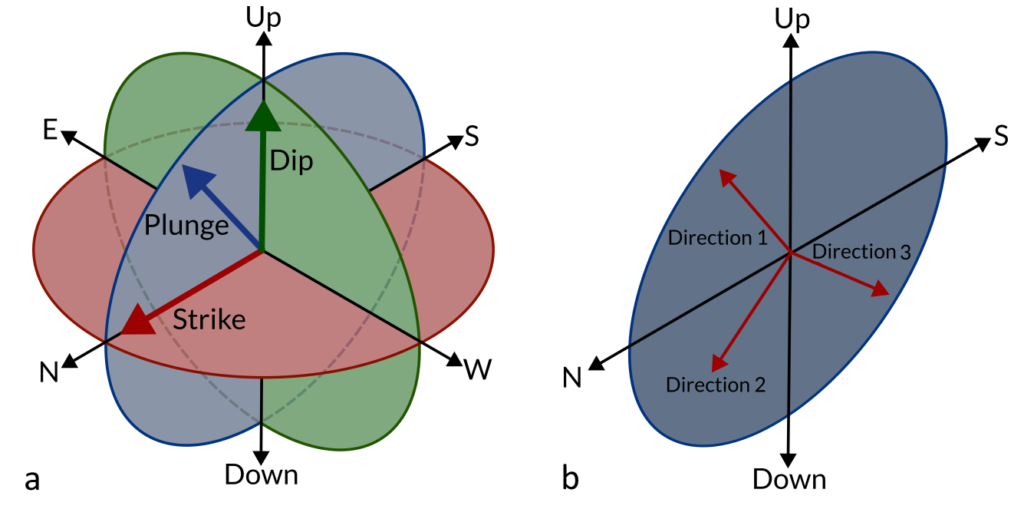
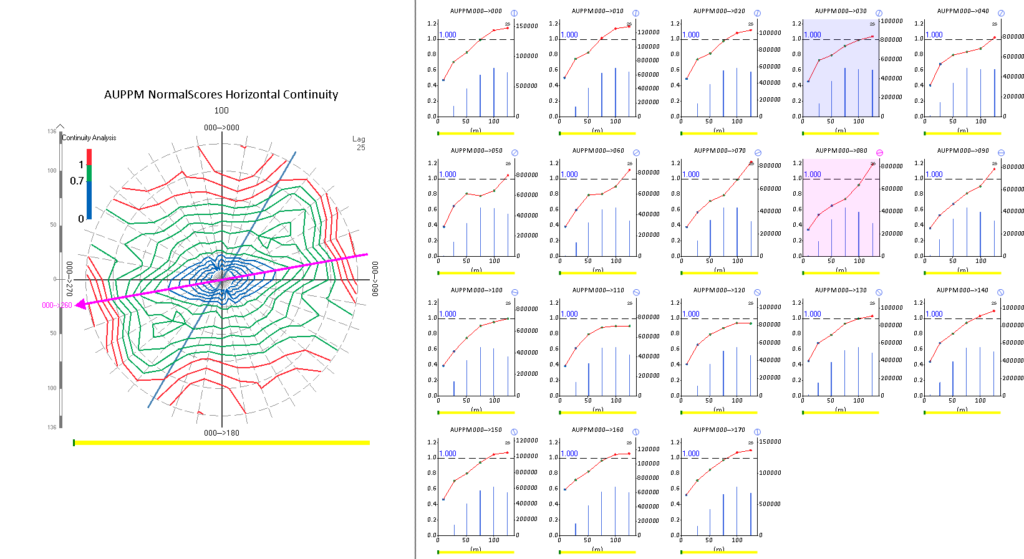
Geological knowledge is the best guide to defining your directions of continuity and all directions should be assessed to ensure they make geological sense. Variogram fans are a useful tool to confirm these directions or define them if there is insufficient geological information.

Interpreting

Once the three orthogonal directions have been determined, then the variograms need to be interpreted and a variogram model fitted to each direction. This allows variogram values to be calculated by the estimation software for any separation distance in any direction. There are several variogram models with different shapes, including spherical, exponential, Gaussian, and hole-effect models. The most common models are spherical and exponential. The goal is to choose a model that accurately reflects the experimental variogram. Standard model shapes can be accumulated to create more detailed variogram model shapes, which are commonly referred to as nested variogram models. Simplicity is key when using nested models, minimizing unnecessary complexity.

Variogram Features

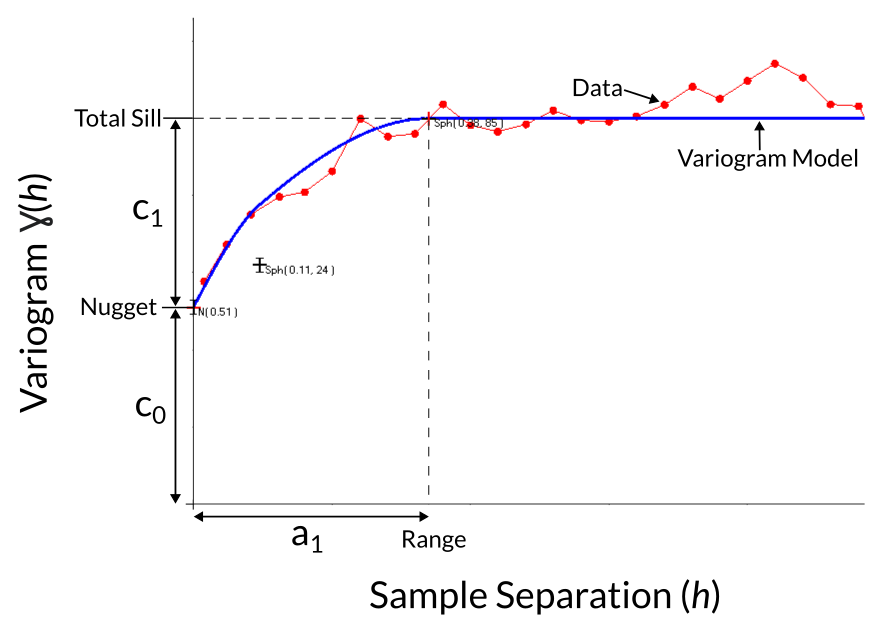
Variogram models have three main features:

• The nugget effect (c_O), which describes the expected difference between samples when the separation distance is almost zero. The nugget effect could be attributed to inherent small scale (geological) variability or any errors in the data (e.g. sampling errors and database errors).
• The total sill (c_O+c₁), which represents the total variability inherent in the data. The sill is equivalent to the total data variance that would be calculated using the variance statistic, although most variograms are standardised to a total sill of 1 for simplicity.
• The range (a₁) of continuity is the lag or separation distance at which the variability reaches the sill. When samples are separated by distances beyond the range of continuity they have no spatial correlation.

Connecting the Dots in Variogram Interpretation

Interpreting variograms can be complex but following a few key rules can ensure accuracy and consistency. When defining a three-dimensional model of grade continuity, it’s crucial that the models in all three orthogonal directions have the same nugget effect and sill values. This also means using the same number of nested structures and model types. Supervisor links the nugget effect and sill values between the three directions, along with the model type and number of structures, to ensure that these rules are followed. The nugget effect plays a vital role in the variogram model and significantly affects sample weights and estimates. Ideally, the closest spaced data, which is typically in the downhole direction, should be used to model the nugget value. Supervisor’s downhole variogram, generated using the hole ID as a key field, provides the best estimation of the nugget effect. Once the nugget effect is accounted for, it’s time to focus on modelling the grade continuity in all three directions. By adjusting the variogram models with interactive sliders, a reasonable fit can be achieved for each direction.

In cases where skewed distributions are present, such as gold grades in gold deposits, extreme high-grade outliers can distort the variogram calculation and obscure the underlying continuity. It is recommended to transform the data prior to calculating variograms using normal scores or indicator transforms. Both of these transforms, along with the required back transform of the normal scores variogram model sill values, can be performed easily in Supervisor.

With Supervisor, modelling variograms becomes effortless, efficient, and intuitive. Multiple windows allow simultaneous viewing and modelling of variograms in all directions, in both 2D and 3D. Supervisor also offers auto-fitting of variogram models and interactive adjustment of lags, enabling quick testing and ensuring the stability of your model.

Summary

We hope that you found this comprehensive guide to variography helpful, exploring its core principles and importance in geostatistical analysis. We’ve explored every stage of variogram analysis, from preparation to interpretation, all while providing crucial insights to effectively harness this essential technique using Supervisor!

If you want to learn more about preparing and analysing variograms using Supervisor, check out Snowden Optiro website for more information about our hands-on professional development course: Practical Variography Using Supervisor. It’s a great opportunity to expand your skills and make variography an integral part of your toolkit.